How fair art thou?
I could never get over this nagging suspicion that my least favourite skittle colour, yellow, popped up more than the other ones. And so I did my solemn data analyst’s duty, and recorded the data… before forgetting about it for a long time.
Fast forward to two whole years later, and as I was deleting some old files, I came across the spreadsheet I had been keeping.
Well, the time has come to address this once and for all. Now, skittle counting seems to have a long and illustrious history on the internet, so I won’t be the first to go down this road. But instead of tearing open a hundred packets, we’ll go about this analysis in a different way.
First, let’s look at our gathered data. Each of the 9 rows is an individual bag, complete with batch number, date, and the count of respective colours.
## # A tibble: 9 x 9
## Batch Date Orange Yellow Green Red Purple Total Size
## <chr> <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 16 02 20 / 171 A 24P 2018-07-09 15 11 6 11 6 49 55g
## 2 16 02 20 / 171 A 24P 2018-07-10 10 9 7 10 13 49 55g
## 3 16 02 20 / 171 A 24L 2018-07-10 11 10 16 6 7 50 55g
## 4 16 02 20 / 171 A 24P 2018-07-11 8 6 9 15 12 50 55g
## 5 16 02 20 / 171 A 24L 2018-07-12 11 7 8 8 16 50 55g
## 6 16 02 20 / 171 A 24L 2018-07-30 7 10 13 13 7 50 55g
## 7 16 02 20 / 171 A 24L 2018-07-31 11 15 14 6 6 52 55g
## 8 16 02 20 / 171 A 24L 2018-08-02 12 13 5 12 8 50 55g
## 9 16 02 20 / 171 A 24L 2018-08-07 8 14 8 13 7 50 55gIf we were to generate a quick summary statistic, we’d get the following:
ObservedSkittlesDistribution## # A tibble: 5 x 2
## Colour mean
## <chr> <dbl>
## 1 Green 9.56
## 2 Orange 10.3
## 3 Purple 9.11
## 4 Red 10.4
## 5 Yellow 10.6Now the question becomes, given a completely random process of making and bagging skittles, is that value for yellow suggestive of a bias? We can arrive to this answer in a few different ways. The traditional method would be to use mathematical functions, but in this case, we’ll use a statistical computing approach and simulate a completely random skittles factory that generates and bags skittles in a normally distributed way. We’ll know this for sure because we’ll code it to be completely fair!
Building a Skittles Factory!
Let’s simulate making 100,000 bags of 50 skittles each. To fill the bags, we’ll sample with replacement from the five colours available. Since no custom probability argument is provided for R’s default sample function, it will give each colour the same probability of being drawn.
sims <- crossing(sim = 1:100000,
skittle = 1:50)
sims <- sims %>% mutate(colour = sample(c("Yellow", "Red", "Orange", "Green", "Purple"),
size = nrow(sims),
replace = TRUE))What we end up with is a 5 million row long dataframe, of 100,000 simulations, with each simulation comprising of 50 skittles.
head(sims)## # A tibble: 6 x 3
## sim skittle colour
## <int> <int> <chr>
## 1 1 1 Purple
## 2 1 2 Purple
## 3 1 3 Yellow
## 4 1 4 Green
## 5 1 5 Yellow
## 6 1 6 RedTo make the data easier to analyse, we can then group by each simulation and colour, and count the number of skittles:
gathered <- sims %>%
group_by(sim, colour) %>%
summarise(n = n())## `summarise()` has grouped output by 'sim'. You can override using the `.groups` argument.gathered## # A tibble: 499,987 x 3
## # Groups: sim [100,000]
## sim colour n
## <int> <chr> <int>
## 1 1 Green 10
## 2 1 Orange 7
## 3 1 Purple 10
## 4 1 Red 10
## 5 1 Yellow 13
## 6 2 Green 8
## 7 2 Orange 10
## 8 2 Purple 14
## 9 2 Red 11
## 10 2 Yellow 7
## # ... with 499,977 more rowsThe beauty of this approach is that now, we have the ability to plot a probability mass function of the distribution of any skittle colour. So for example, we can draw a histogram of the observed distributions for yellow, together with the mean count of yellow from our observed data (black line):
yellowMean <- ObservedSkittlesDistribution %>%
filter(Colour == "Yellow") %>% pull(mean)
Yellow <- gathered%>%
filter(colour == "Yellow") %>%
ggplot(aes(n)) +
geom_histogram(fill = "#FEEE22", bins = 70)+
geom_vline(xintercept = yellowMean)+
theme_bw()+
labs(title = "Values of Yellow Skittles if distribution was due to chance vs. Observed",
subtitle = "100,000 simulations")+
xlab("Yellow Skittles per Bag") +
ylab("Bags")
Yellow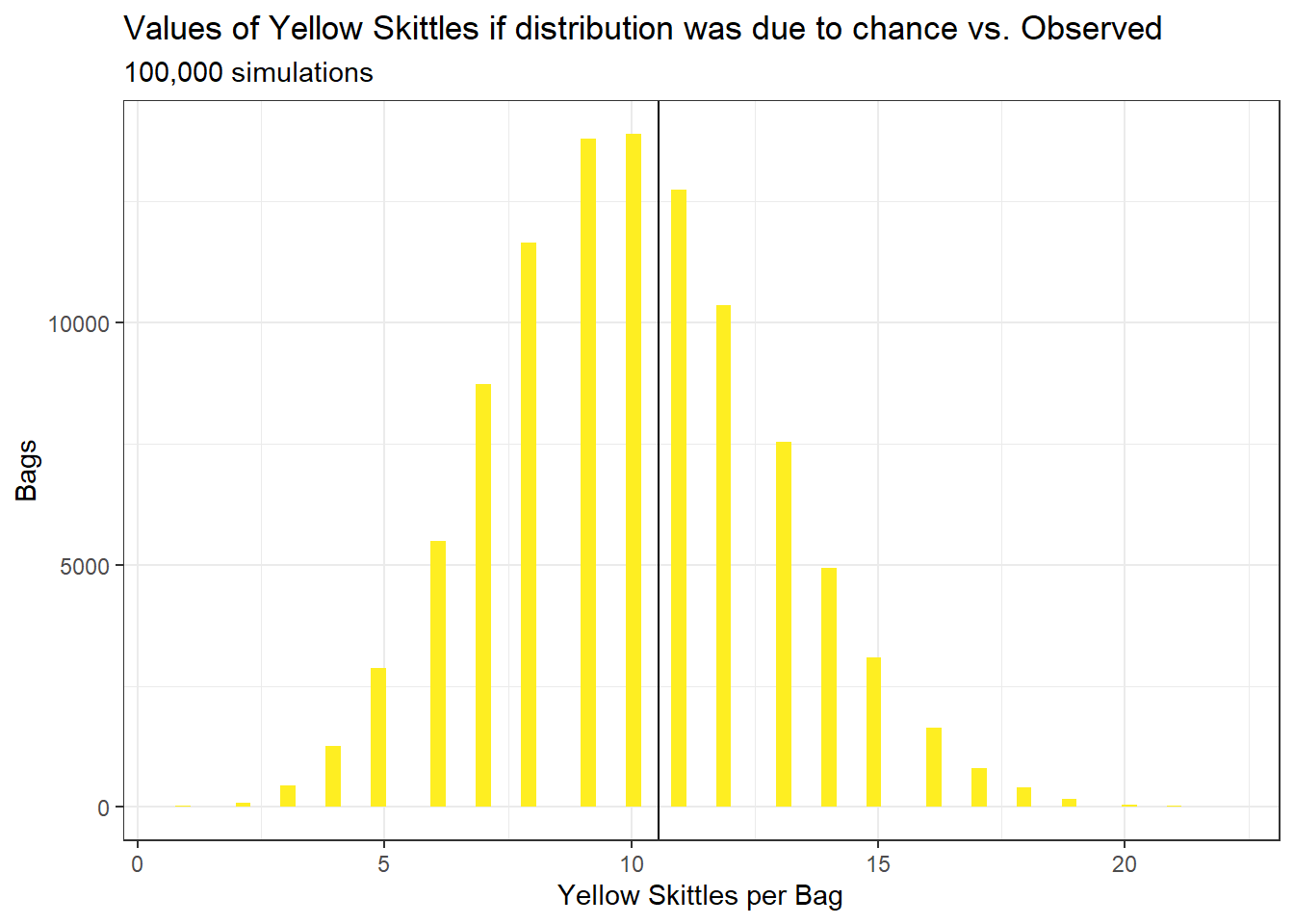
What we can see is that in a perfectly random process, the most common number of yellow skittles is 10, matching with the commonsense probability of 1/5 * 50. Yet, this is only the case for 13,000 bags out of 100,000. In other instances, it can be a bit off to each side, and in some extreme cases, we might have as few as 2 yellow skittles and as many as 20 yellow skittles in a single bag.
This is also a great visual display of what a p-value really is: the probability of observing a result this extreme given a null distribution. What’s more, to get a p-value out of this, all we’d need to do is count the number of times the mean of yellow skittles we observed (10.5) is greater than the number of times we’d get a bag with 10.5 skittles or more. Or in R terms:
sum(yellowMean >= gathered %>% filter(colour == "Yellow") %>% pull(n))/100000## [1] 0.58249Which tells us that we’d observe a value this extreem in 58% of the cases, even if the skittles factory was completely fair.
Simulations like these also make it easy to calculate quantiles.
gathered %>%
group_by(colour) %>%
summarise(lowerQ = quantile(n, probs = 0.025),
upperQ = quantile(n, probs = 0.975))## # A tibble: 5 x 3
## colour lowerQ upperQ
## <chr> <dbl> <dbl>
## 1 Green 5 16
## 2 Orange 5 16
## 3 Purple 5 16
## 4 Red 5 16
## 5 Yellow 5 16We can then say that in 95% of the bags we open, we’ll have no less than 5 or no more than 16 skittles of each colour. They’re all identical because with our 100,000 simulations, the law of large numbers has started to apply.